相信我,把他看完就是奇迹。
Step1 by Miuc @ 12.18/2009
二元运算 集合S上的二元运算必须满足:
a.可运算性, 任意两个元素都可以进行运算
b.单值性, 运算的两个元素生成值唯一
c.封闭性, 运算产生结果仍在S内
由定义知,自然数N上的减法运算不是二元运算,不满足封闭性。实数集R上的除法由于0不能作为除数也不能成为二元运算。
+ – * / 只是作为二元运算的替代符号存在
交换率( xRy = yRx ),结合率( (xRy)Rz = xR(yRz) )与幂等率( xRx=x )
零元,逆元,单位元的唯一性
代数系统 由非空集合S与定义在S上的f1,f2,….fm一元或二元运算称为一个代数系统。
群 群总体上说是“众多只与一个二元运算结合的代数系统中最重要的一种”。
群论是代数系统中古老而又丰富的分支。
设对于在非空集合上的二元运算符来说,运算具有结合性,称其与集合组成半群。
半群内如果存在单位元,则称其为幺半群。
对于半幺群,如其内任意元素具有逆元,则其称为群。
设对于群G上交换率成立,则称G为交换群或阿贝尔(Abel)群。
群G的阶|G|为其基数(集合内元素个数)。
群G中元素a的阶为使a^k = e 成立的最小正整数k。
设群< G , * >内有非空子集H满足*构成群,则称H<=G,H为G的子群。
子群三大判定定理:
1. H <= G iff a,b ∈H && a*b ∈H && a^-1 ∈H
2. H <= G iff a,b ∈H && a*b^-1 ∈H
3.H <= G iff a,b ∈H && a*b ∈H
设H为群G子群,如果对于任意a ∈ G 有 Ha = aH,称H是G的正规子群。
Ha 为子群H在G中的右陪集,aH为子群H在G中的左陪集。
商群 给定一个群G和G的正规子群N,G在N上的商群或因子群,可以作为把G划分至包含单位元的群。
商群写为 G/N 并念作 G mod N,如果N不是正规子群,则结果不是群,而是齐次空间。
我们定义集合 G/N 是 N 在 G 中的所有左陪集的集合,就是说 G/N = { aN : a∈G }
而 (aN)(bN) = a(Nb)N = a(bN)N = (ab)NN = (ab)N
所以 G/N 也可以定义为 N 在 G 中所有的右陪集的集合
因为运算是从 G 的子集的乘积得出的,这个运算是良好定义的(不依赖于表示的特定选择),符合结合律的,并有单位元 N。G/N 的元素 aN 的逆元是 a−1N。
商群定义的动机
G/N 叫做商群的理由来自整数的除法。
在 12 除以 3 的时候得到答案 4 是因为我们可以把 12 个对象重现分组为 3 个对象的 4 个子搜集。
商群出于同样想法,但用一个群作为最终答案而非一个数,因为群要比对象的随机搜集要更有结构。
更进一步,我们查看G/N时,这个群构成一种自然的重新分组,可以想想将一个集合归纳与一个最小结构。
群同态属于群向高端数学起步的基点,数学上,一个态射是两个数学结构之间保持结构的过程的一种抽象。
最常见的这种过程的例子是在某种意义上保持结构的函数或映射。
例如,在集合论中,态射就是函数,在群论中,它们是群同态,而在拓扑学中,它们是连续函数。
在泛代数(universal algebra)的范围,态射通常就是同态。
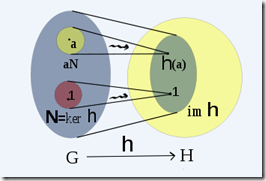
我们定义 h 的核为被映射到 H 中单位元上的 G 中的那些元素的集合
ker(h) = { u ∈ G : h(u) = e in H } // G上所有能通过h映射至H的单位元的元素
定义 h 的像为
- im(h) = { h(u) : u ∈ G } // G通过h生成的像
群同态基本定理:
群同态第一基本定理
如果f是群G到群H的一个群同态,则
- f的核(kernel)K是G的正规子群;
- 商群G/K群同构于f的像(image);
- f的像是H的子群。
群同态第二基本定理
如果H和K是群G的子群,H是K的正规化子的子群,则
- H与K的乘积HK是G的子群;
- K是HK的正规子群,H∩K是H的正规子群;
- HK/K同构于H/(H∩K)。
群同态第三基本定理
如果M、N是G的正规子群,M属于N,那么
- M是N的正规子群;
- N/M是G/M的正规子群;
- (G/M)/(N/M)同构于G/N。
未完待续,上离散课,回来继续,下一步:继续群同态。
参考资料: 武汉大学信安数学课件,Wiki百科