－ － 部分翻译
Elliptic curve cryptography
From Wikipedia, the free encyclopedia
Elliptic curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz[ 1] and Victor S. Miller[ 2] in 1985.
Elliptic curves are also used in several integer factorization algorithms that have applications in cryptography, such as Lenstra elliptic curve factorization.
椭圆曲线加密技术 (ECC) 是一种基于椭圆曲线的代数在有限域上的公共密钥加密技术。
基于因数分解问题的因数分解密码系统，典型代表为RSA；基于离散对数问题的离散对数密码系统，典型代表为DSA;
基于椭圆曲线离散对数问题的椭圆曲线密码系统（ECC）;
{以上非原创。}
Contents[hide ] |
[edit] Introduction 介绍
Public-key cryptography is based on the intractability of certain mathematical problems. Early public-key systems, such as the RSA algorithm , are secure assuming that it is difficult to factor an integer with two large prime factors. For elliptic-curve-based protocols, it is assumed that finding the discrete logarithm of an elliptic curve element is infeasible. The size of the elliptic curve determines the difficulty of the problem. It is believed that a smaller group can be used to obtain the same level of security as RSA-based systems. Using a small group reduces storage and transmission requirements.
An elliptic curve is a plane curve which consists of the points satisfying the equation
y 2 = x 3 + a x + b ,
along with a distinguished point at infinity, denoted 
. This set forms an Abelian group, with the point at infinity as identity element. If the coordinates x and y are chosen from a finite field, the solutions form a finite abelian group.
As for other popular public key cryptosystems, no mathematical proof of difficulty has been published for ECC as of 2009[update] . However, the U.S. National Security Agency has endorsed ECC technology by including it in its Suite B set of recommended algorithms and allows their use for protecting information classified up to top secret with 384-bit keys.[ 3] Although the RSA patent has expired, there are patents in force covering certain aspects of ECC implementation, though some argue that a practical ECC key exchange system can be implemented without infringing them.[ 4]
公共密钥加密技术基于某些极端的数学问题。
基于椭圆曲线的协议中假定无法发现椭圆曲线元素的离散对数。
特征值P=2时，有 y 2 + xy = x 3 + a x 2 + b
或 y 2 + ay = x 3 + b x + c
特征值P=3时，有 y 2 = x 3 + b(1) x 2 +b(2)x + b(3) 。
特征值P!=2,3时，有 y 2 = x 3 + a x +b
{同样非原创}
[edit] Cryptographic schemes 加密方案
Several RSA-based protocols have been adapted to elliptic curves, replacing the group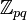 
with an elliptic curve:
- the Elliptic Curve Diffie-Hellman key agreement scheme is based on the Diffie-Hellman scheme,
- the Elliptic Curve Digital Signature Algorithm is based on the Digital Signature Algorithm,
- the ECMQV key agreement scheme is based on the MQV key agreement scheme.
At the RSA Conference 2005, the National Security Agency (NSA) announced Suite B which exclusively uses ECC for digital signature generation and key exchange. The suite is intended to protect both classified and unclassified national security systems and information.[ 5]
Recently, a large number of cryptographic primitives based on bilinear mappings on various elliptic curve groups, such as the Weil and Tate pairings, have been introduced. Schemes based on these primitives provide efficient identity-based encryption as well as pairing-based signatures, signcryption, key agreement , and proxy re-encryption [1] .
[edit] Implementation considerations 实施注意事要
Although the details of each particular elliptic curve scheme are described in the article referenced above some common implementation considerations are discussed here.
[edit] Domain parameters 域参数
To use ECC all parties must agree on all the elements defining the elliptic curve, that is, the domain parameters of the scheme. The field is defined by p in the prime case and the pair of m and f in the binary case. The elliptic curve is defined by the constants a and b used in its defining equation. Finally, the cyclic subgroup is defined by its generator (aka. base point ) G . For cryptographic application the order of G , that is the smallest non-negative number n such that n G = O , must be prime. Since n is the size of a subgroup of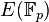 
it follows from the Lagrange’s theorem that the number 
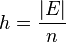is an integer. In cryptographic applications this number h , called the cofactor , at least must be small (
) and, preferably, h = 1 . Let us summarize: in the prime case the domain parameters are (p ,a ,b ,G ,n ,h ) and in the binary case they are (m ,f ,a ,b ,G ,n ,h ) .
Unless there is an assurance that domain parameters were generated by a party trusted with respect to their use, the domain parameters must be validated before use.
The generation of domain parameters is not usually done by each participant since this involves counting the number of points on a curve which is time-consuming and troublesome to implement. As a result several standard bodies published domain parameters of elliptic curves for several common field sizes:
- NIST, Recommended Elliptic Curves for Government Use
- SECG, SEC 2: Recommended Elliptic Curve Domain Parameters
Test vectors are also available [2] .
If one (despite the said above) wants to build his own domain parameters he should select the underlying field and then use one of the following strategies to find a curve with appropriate (i.e., near prime) number of points using one of the following methods:
- select a random curve and use a general point-counting algorithm, for example, Schoof’s algorithm or Schoof-Elkies-Atkin algorithm ,
- select a random curve from a family which allows easy calculation of the number of points (e.g., Koblitz curves), or
- select the number of points and generate a curve with this number of points using complex multiplication technique.[ 6]
Several classes of curves are weak and shall be avoided:
- curves over
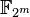with non-prime m are vulnerable to Weil descent attacks.[ 7] [ 8] - curves such that n divides p B − 1 (where p is the characteristic of the field – q for a prime field, or 2 for a binary field) for sufficiently small B are vulnerable to MOV attack[ 9] [ 10] which applies usual DLP in a small degree extension field of
to solve ECDLP. The bound B should be chosen so that discrete logarithms in the field 
are at least as difficult to compute as discrete logs on the elliptic curve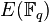 
.[ 11] - curves such that
are vulnerable to the attack that maps the points on the curve to the additive group of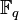 
[ 12] [ 13] [ 14]
SECI 及 IEEE P1363 工作草案中 定义椭圆曲线域参数由一个六元偶 T= ( P ,a ,b ,G ,n ,h ) 组成。
其中我们使用 P 表示 有限域 Eq , 或者 m 表示 F2m
二元素 a,b属于Fq
由此可以确定一条椭圆曲线，g表示一个基点，n为其对应的阶。 h=#E(Fq)/n, 为一个小整数。
[edit] Key sizes 密钥大小
Since all the fastest known algorithms that allow to solve the ECDLP (baby-step giant-step, Pollard’s rho, etc.), need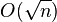 
steps, it follows that the size of the underlying field shall be roughly twice the security parameter. For example, for 128-bit security one needs a curve over 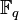, where 
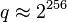. This can be contrasted with finite-field cryptography (e.g., DSA) which requires[ 15] 3072-bit public keys and 256-bit private keys, and integer factorization cryptography (e.g., RSA ) which requires 3072-bit public and private keys. The hardest ECC scheme (publicly) broken to date had a 109-bit key (that is about 55 bits of security). For the prime field case, it was broken near the beginning of 2003 using over 10,000 Pentium class PCs running continuously for over 540 days (see [3] ). For the binary field case, it was broken in April 2004 using 2600 computers for 17 months (see [4] ).
一般的，我们可以认为，当Q的长度为160bit时，其安全性相当于RSA使用1024bit长的密码。
[edit] Projective coordinates 投影坐标
A close examination of the addition rules shows that in order to add two points one needs not only several additions and multiplications in 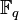but also an inversion operation. The inversion (for given 
find 
such that x y = 1 ) is one to two orders of magnitude slower[ 16] than multiplication. Fortunately, points on a curve can be represented in different coordinate systems which do not require an inversion operation to add two points. Several such systems were proposed: in the projective system each point is represented by three coordinates (X ,Y ,Z ) using the following relation: 
, 
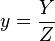; in the Jacobian system a point is also represented with three coordinates (X ,Y ,Z ) , but a different relation is used: 
, 
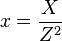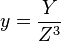; in the López-Dahab system the relation is , 
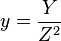; in the modified Jacobian system the same relations are used but four coordinates are stored and used for calculations (X ,Y ,Z ,a Z 4 ) ; and in the Chudnovsky Jacobian system five coordinates are used (X ,Y ,Z ,Z 2 ,Z 3 ) . Note that there may be different naming conventions, for example, IEEE P1363-2000 standard uses “projective coordinates” to refer to what is commonly called Jacobian coordinates. An additional speed-up is possible if mixed coordinates are used.[ 17]
[edit] Fast reduction (NIST curves) 快速缩小 － － 还是叫 Fast reduction吧..
Reduction modulo p (which is needed for addition and multiplication) can be executed much faster if the prime p is a pseudo-Mersenne prime that is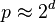 
, for example, p = 2521 − 1 or p = 2256 − 232 − 29 − 28 − 27 − 26 − 24 − 1 . Compared to Barrett reduction there can be an order of magnitude speed-up.[ 18] The curves over with pseudo-Mersenne p are recommended by NIST. Yet another advantage of the NIST curves is the fact that they use a = − 3 which improves addition in Jacobian coordinates.
The speedup here is a practical rather than theoretical one, and derives from the fact that the moduli of numbers against numbers near powers of two can be performed efficiently by computers operating on binary numbers with bitwise operations.
[edit] NIST-recommended elliptic curves NIST 推荐椭圆曲线方法
NIST recommends fifteen elliptic curves. Specifically, FIPS 186-2 has ten recommended finite fields. There are five prime fields for p 192 , p 224 , p 256 , p 384 and p 521 . For each of the prime fields one elliptic curve is recommended. There are five binary fields 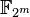for 2163 , 2233 , 2283 , 2409 , and 2571 . For each of the binary fields one elliptic curve and one Koblitz curve was selected. Thus five prime curves and ten binary curves. The curves were chosen for optimal security and implementation efficiency.[ 19]
推荐了几种椭圆曲线。
[edit] Side-channel attacks 侧信道攻击
Unlike DLP systems (where it is possible to use the same procedure for squaring and multiplication) the EC addition is significantly different for doubling (P = Q ) and general addition (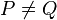
) depending on the coordinate system used. Consequently, it is important to counteract side channel attacks (e.g., timing or simple/differential power analysis attacks) using, for example, fixed pattern window (aka. comb) methods[ 20] (note that this does not increase the computation time). Another concern for ECC-systems is the danger of fault attacks, especially when running on smart cards, see for example Biehl et. al[ 21] .
[edit] Patents ….
At least one ECC scheme (ECMQV ) and some implementation techniques are covered by patents. Uncertainty about the availability of unencumbered ECC has limited the acceptance of ECC.
